Tools developed by the CHARM Mazurka project
Andrew Earis and Craig Sapp of the CHARM project Style, performance, and meaning in Chopin's Mazurkas developed a range of software tools for capturing tempo, dynamics, and articulation data from recordings (particularly of piano music), and for analysing the data in order to display stylistic features; these are available on this site, together with a large quantity of data and analytical visualisations. These materials are located on the Mazurka project website. Here we provide a brief guide to what they are and how they might be used.
Tools for data capture
For many musicological purposes, including much of the work on the CHARM Mazurka project, it is perfectly satisfactory to obtain tempo data by tapping along to the music using Sonic Visualiser; the data will not be perfectly accurate, since what is actually being measured is not the sound but your physical response to it - which is why we call this 'reverse conducting' - but it will still support a wide range of music-analytical observations. (Sapp has conducted extensive studies into the accuracy and reliability of this data: see his pages entitled Reverse conducting example, Reverse conducting evaluation, Metric analysis of tapping accuracy, and Experiments.) As detailed in A musicologist's guide to Sonic Visualiser, once you have your tempo data you can easily generate dynamic data using a plugin, or obtain average dynamic values for each beat using Dyn-A-Matic, an online tool developed by Sapp; again there are limitations in the accuracy and psychological reality of the data (because we hear sounds as discrete streams, not globally), but used sensibly it can still support a range of music-analytical observations.
Another online tool developed by Sapp, Tap Snap, may help you refine your data. You upload your tapped timings from Sonic Visualiser, together audio onset data generated by the MzSpectralReflux plugin, and Tap Snap shifts the taps so that they align with the nearest onset. You can then import the data back into Sonic Visaliser and assess its accuracy by ear. An advantage of getting your timing data as accurate as possible is that it improves the results from Dyn-A-Matic, which is very sensitive to timing accuracy.
We have also developed a system which can capture timing and dynamic values for every individual note. Andrew Earis' Expression Algorithm software does this, but at the expense of being more complicated in use. This program takes as its input both a sound file and a 'notes' file containing tapped tempo data (this keeps the algorithm on track); the output is a series of files containing timing, dynamic, and articulation information for each note, which can be imported into a spreadsheet or otherwise manipulated for further analysis. It should be noted that the evaluation of both dynamic and articulation data depends on a number of assumptions and approximations that do not necessarily correspond to human perception, so that his information must again be used with care. Click here for instructions on how to download, install, and use the Expression Algorithm software.
Tools for analysis
During his doctoral studies at Stanford, Sapp developed a means of representing harmonic structure through what he called keyscapes: triangular figures in which the base corresponds to the moment-to-moment course of the music, with successively higher layers showing averaged values based on the layer below, with the apex of the triangle consisting of a single value representing the average value for the piece as a whole. The result is to provide a visual impression of the strength of particular hamonies at particular points in the music at both a local and global level.
Keyscapes are based on score data, not performance values, but Sapp adapted this approach for the representation of tempo and dynamic information, giving rise to what we call ‘timescapes’ and ‘dynascapes’. These are based on numerical values corresponding to each beat, the value representing tempo or duration in the case of timescapes, and global dynamics in the case of dynascapes. Each can take a number of forms, of which two are probably most useful.
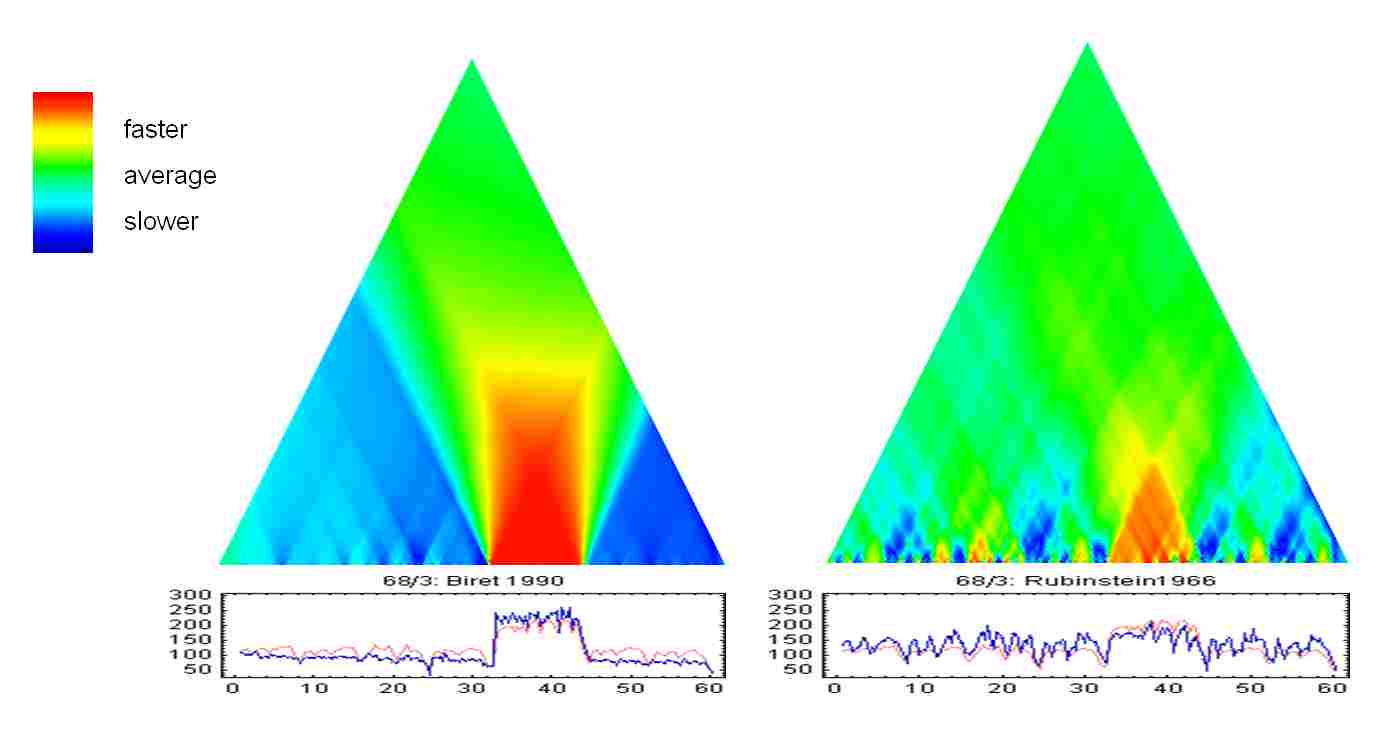
The first is ‘Average’ scapes. These provide a view of the pattern of tempo or dynamic change across the performance: the lower rows show localised features, while higher rows show increasingly large-scale features. The examples below come from Cook's 'Performance analysis and Chopin's mazurkas' (Musicae Scientiae 11/2 [2007], 183-207), and represent tempo relations in Chopin's Mazurka Op. 68 No. 3 as recorded by Idil Biret (1990) and Artur Rubinstein (1966): they show how Biret plays without a great deal of rubato, taking the middle section at a much higher tempo, whereas Rubinstein's performance is full of light and shade, consequently de-emphasising the contrast between the middle section and the rest of the piece. Of course this information is already in the tempo graph below the timescape (in which the faint red line represents the average for all our recordings of that Mazurka), but the timescape presentation brings out particular aspects of it, especially at larger levels such as phrasing.
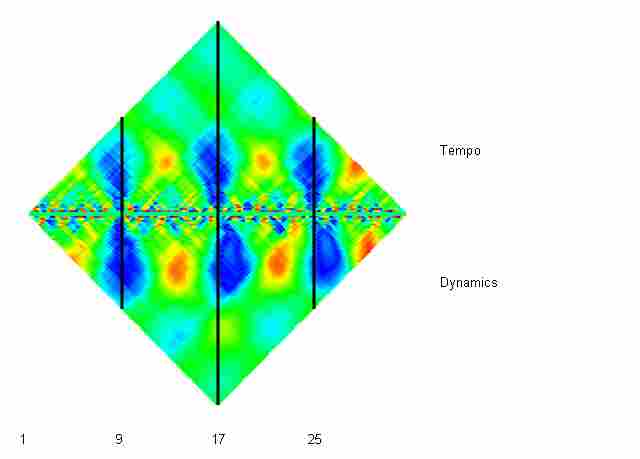
The second particularly useful kind of scape is the ‘Arch’ scape which works in a quite different way: it searches the tempo or dynamic data for evidence of phrase arching, using Pearson correlation. The arch timescape below represents Heinrich Nauhaus's 1955 recording of bars 1-32 of Chopin's Mazurka Op. 63 No. 3, with the red-orange flames showing rising arches (getting louder and faster), and the blue ones showing falling arches (getting softer and slower): it shows how Nauhaus creates a series of very regular phrase arches, almost exactly coordinated between tempo and dynamics (hence the bilateral symmetry). This figure, from Cook’s chapter in the Cambridge Companion to Recorded Music, was created by generating tempo and dynamic scapes separately, and then joining and annotating them using a drawing program.
An explanation of timescapes and dynascapes, with examples, may be found on the Hierarchical Correlation Plots page, and you can generate your own using the online Scape plot generator. To create an Average scape, simply paste in your tempo or dynamic data and click on Submit; to create an Arch scape, click on Arch Correlation before Submit.
Tempo and dynamic profiles result from a number of possibly independent musical factors, for instance the patterns of small-scale accentuation that give rise to the ‘Mazurka’ effect as against such large-scale features as phrase arching. For this reason it can be helpful to separate out the note-to-note details from the larger shapes, and a simple way of doing this is by means of smoothing: you use a mathematical smoothing function to eliminate the note-to-note details, leaving the larger smoothed profile, and then you can subtract the smoothed profile from the original data, leaving just the note-to-note details (we call this ‘desmoothed’ or ‘unsmoothed’ data, though the correct mathematical term is ‘residual’). You can then adopt different analytical approaches for each set of data. Our online Data smoother generates smoothed and desmoothed data in a single operation, using an algorithm that avoids the shifting normally found in spreadsheet smoothing functions.
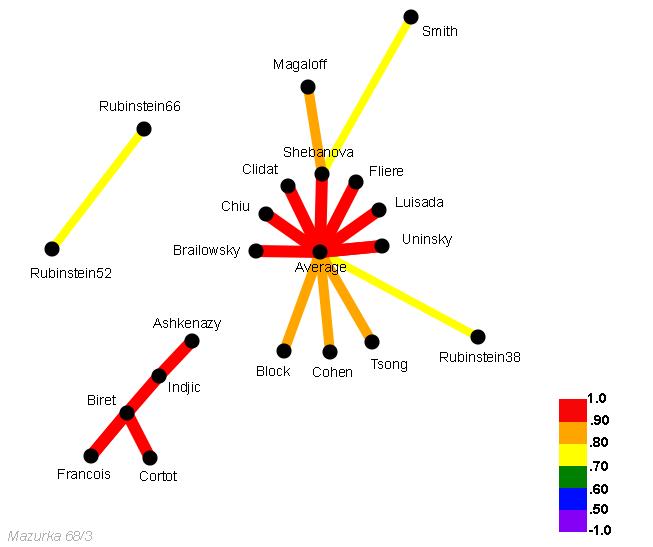
A way of graphically representing relationships between a number of different recorded performances of the same piece is the Correlation network, in which performances are linked by lines whose weight and/or colour represent how similar they are; the example below is again taken from Cook’s 'Performance analysis and Chopin's mazurkas'.
Such diagrams merely represent mathematical relationships between two series of numbers, representing tempi/durations or global dynamics as the case may be, and to treat them as definitive evidence of perceived similarity or influence would be highly naive. Used with care, however, they can be a convenient way in which to represent large quantities of data. You can generate your own diagrams using the online Correlation Network Diagram Generator; an attractive feature of the resulting plots is that you can drag the network into whatever shape best brings out the connections you have found, while a less attractive feature is that you have to add the labels identifying each performance manually. This feature only works if you are using the Mozilla Firefox web browser.
As a means of representing tempo or global dynamic correlations between different recordings, a major limitation of Correlation networks is that they simply give you a single value. But a performance may resemble another performance at one particular point, and not at another. For this reason a more powerful way of representing relationships is through a further development of the scape representation, which shows the similarity between performers at different parts of the performance and at different hierarchical levels. This is illustrated by an extensive gallery of correlation plots of performances of Opp. 17 No. 4, 24 No. 2, 30 No. 2, 63 No. 3, and 68 No. 3, based on both smoothed and desmoothed tempo and dynamic data: they can be accessed by performer or by individual mazurka. As an example, the tempo correlation plot for Rieko Nezu's 2005 recording of Chopin's Mazurka Op. 24 No. 2, shown below, assigns a different colour to each recording. On the web page from which it is taken, the colour codes are shown below the plot, followed by four columns of similarity measurements. The first column, marked '0-rank 0-score', represents the global correlation value between the reference performer (Nezu) and the others: the first row says that the correlation between the recordings by Nezu and Ashkenazy is 0.72, and that this value is the twenty-first best correlation in the list. The most robust similarity measurements appear to be those shown in the '4-score 4-rank' column. Further information on this method may be found in Sapp's article 'Hybrid numeric/rank similarity metrics for musical performance analysis'.
Although they are based on scape technology, it is not possible to generate these complex correlation plots using the online Scape plot generator. It should of course be born in mind that these are objectively generated rather than culturally interpreted representations; they may or may not correspond to the influence of one performer on another, to listeners' perceptions of similarity, and so forth. But that is the whole point. As with other work in the field of Music Information Retrieval (MIR), the basic research question is how far it may, or may not, be possible to model musically meaningful relationships on the basis of purely objective analysis.
Data
The Mazurka project website contains a considerable amount of tempo and global dynamic data in a number of formats, which you may wish to use in trying out the software described above, or for your own work. (We make no restrictions on its use, except that we ask that you acknowledge the source in any resulting publication.) The following is a selective guide to what is available.
- Reverse conducting (i.e. tapping) data, corrected using 'Tapsnap', may be accessed in a variety of formats from http://mazurka.org.uk/info/revcond/#06-1. One of these formats is the 'notes' file used for Andrew Earis's Expression Algorithm software.
- For many purposes the most convenient format in which to access the data is as Excel spreadsheets; tempo data in this format for a large number of recordings of Opp. 17 No. 4, 24 No. 2, 30 No. 2, 63 No. 3, and 68 No. 3 may be found here, and dynamic data here. (To use the data with the online programs, simply copy and paste the relevant part of the spreadsheet.)
- Another useful format in which data for individual recordings is available is annotation files for use with Sonic Visualiser and Audacity, accessible via the Mazurka Audio Markup Page; importing an 'Average tap locations for beats from multiple tapping sessions' file will create bar and beat labels, saving you the trouble of doing your own tapping.
- Finally data for many individual recordings is available via the Mazurka MIDI performance page, in the form of Type 0 and Type 1 MIDI files; there are also MIDI and Match files in the format required for use with Martin Gasser's PerfViz program (a three-dimensional implementation of Simon Dixon, Werner Goebl, and Gerhard Widmer's Performance Worm).